Площадь полной боковой поверхности правильной четырехугольной пирамиды. Как найти площадь боковой поверхности пирамиды
Площадь поверхности пирамиды. В этой статье мы рассмотрим с вами задачи с правильными пирамидами. Напомню, что правильная пирамида – это пирамида, основанием которой является правильный многоугольник, вершина пирамиды проецируется в центр этого многоугольника.
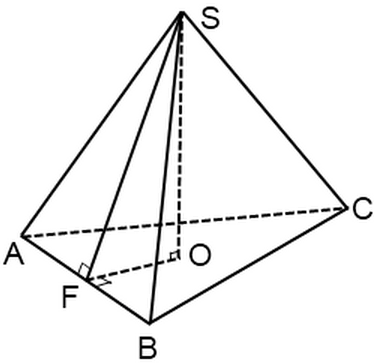
Боковая грань такой пирамиды это равнобедренный треугольник. Высота этого треугольника, проведенная из вершины правильной пирамиды, называется апофемой, SF – апофема:
В представленном ниже типе задач требуется найти площадь поверхности всей пирамиды или площадь её боковой поверхности. На блоге уже рассмотрено несколько задач с правильными пирамидами, где ставился вопрос о нахождении элементов (высоты, ребра основания, бокового ребра), .
В заданиях ЕГЭ, как правило, рассматриваются правильные треугольные, четырёхугольные и шестиугольные пирамиды. Задач с правильными пятиугольными и семиугольными пирамидами не встречал.
Формула площади всей поверхности проста — требуется найти сумму площади основания пирамиды и площади её боковой поверхности:
![]()
Рассмотрим задачи:
Стороны основания правильной четырехугольной пирамиды равны 72, боковые ребра равны 164. Найдите площадь поверхности этой пирамиды.

Площадь поверхности пирамиды равна сумме площадей боковой поверхности и основания:
*Боковая поверхность состоит из четырёх равных по площади треугольников. Основание пирамиды это квадрат.
Площадь боковой стороны пирамиды можем вычислить воспользовавшись :

Таким образом, площадь поверхности пирамиды равна:
Ответ: 28224
Стороны основания правильной шестиугольной пирамиды равны 22, боковые ребра равны 61. Найдите площадь боковой поверхности этой пирамиды.
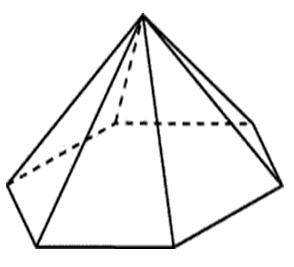
Основанием правильной шестиугольной пирамиды является правильный шестиугольник.
Площадь боковой поверхности данной пирамиды состоит из шести площадей равных треугольников с сторонами 61,61 и 22:
Найдём площадь треугольника, воспользуемся формулой Герона:

Таким образом, площадь боковой поверхности равна:
![]()
Ответ: 3240
*В представленных выше задачах площадь боковой грани можно было найти используя другую формулу треугольника, но для этого нужно вычислить апофему.
27155. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.

Для того, чтобы найти площадь поверхности пирамиды нам необходимо знать площадь основания и площадь боковой поверхности:
Площадь основания равна 36, так как это квадрат со стороной 6.
Боковая поверхность состоит из четырёх граней, которые являются равными треугольниками. Для того, чтобы найти площадь такого треугольника требуется знать его основание и высоту (апофему):
*Площадь треугольника равна половине произведения основания и высоты проведённой к этому основанию.
Основание известно, оно равно шести. Найдём высоту. Рассмотрим прямоугольный треугольник (он выделен жёлтым):

Один катет равен 4, так как это высота пирамиды, другой равен 3, так как он равен половине ребра основания. Можем найти гипотенузу, по теореме Пифагора:
![]()
Значит площадь боковой поверхности пирамиды равна:

Таким образом, площадь поверхности всей пирамиды равна:
Ответ: 96
27069. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
27070. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Существуют ещё формулы площади боковой поверхности правильной пирамиды. В правильной пирамиде основание является ортогональной проекцией боковой поверхности, поэтому:
P - периметр основания, l - апофема пирамиды
*Эта формула основывается на формуле площади треугольника.
Если хотите узнать подробнее как эти формулы выводятся, не пропустите, следите за публикацией статей. На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Определение. Боковая грань - это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).
Определение. Боковые ребра - это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
Определение. Высота пирамиды - это перпендикуляр, опущенный из вершины на основание пирамиды.
Определение. Апофема - это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.
Определение. Диагональное сечение - это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение. Правильная пирамида - это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.
Объём и площадь поверхности пирамиды
Формула. Объём пирамиды через площадь основы и высоту:
Свойства пирамиды
Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.
Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.
Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.
Свойства правильной пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые ребра наклонены под одинаковыми углами к основанию.
4. Апофемы всех боковых граней равны.
5. Площади всех боковых граней равны.
6. Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.
8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n , где n - это количество углов в основании пирамиды.
Связь пирамиды со сферой

Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.

В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Связь пирамиды с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.
Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.
Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.
Связь пирамиды с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.
Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.


В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол .
Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника (GM).
Бимедианой называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.


Определение. Остроугольная пирамида - это пирамида в которой апофема больше половины длины стороны основания.
Определение. Тупоугольная пирамида - это пирамида в которой апофема меньше половины длины стороны основания.
Определение. Правильный тетраэдр - четырехгранник у которого все четыре грани - равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.
Определение. Прямоугольный тетраэдр называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Определение. Равногранный тетраэдр называется четырехгранник у которого боковые грани равны между собой, а основание - правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.
Определение. Ортоцентричный тетраэдр называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.
Определение. Звездная пирамида называется многогранник у которого основой является звезда.

– это фигура, в основании которой лежит произвольный многоугольник, а боковые грани представлены треугольниками. Их вершины лежат в одной точке и соответствуют вершине пирамиды.
Пирамида может быть разнообразной – треугольной, четырехугольной, шестиугольной и т.д. Ее название можно определить в зависимости от количества углов, прилегающих к основанию.
Правильной пирамидой
называется пирамида, в которой равны стороны основания, углы, и ребра. Также в такой пирамиде будет равна площадь боковых граней.
Формула площади боковой поверхности пирамиды представляет собой сумму площадей всех ее граней: ![]()
То есть, чтобы рассчитать площадь боковой поверхности произвольной пирамиды, необходимо найти площадь каждого отдельного треугольника и сложить их между собой. Если пирамида усеченная, то ее грани представлены трапециями. Для правильной пирамиды существует другая формула. В ней площадь боковой поверхности рассчитывается через полупериметр основания и длину апофемы:
Рассмотрим пример расчета площади боковой поверхности пирамиды.
Пусть дана правильная четырехугольная пирамида. Сторона основания b
= 6 см, а апофема a
= 8 см. Найдите площадь боковой поверхности.
В основании правильной четырехугольной пирамиды лежит квадрат. Для начала найдем его периметр:
Теперь можем просчитать площадь боковой поверхности нашей пирамиды:![]()
Для того чтобы найти полную площадь многогранника, потребуется найти площадь его основания. Формула площади основания пирамиды может отличаться, в зависимости от того, какой многоугольник лежит в основании. Для этого используются формулы площади треугольника, площади параллелограмма и т.д.
Рассмотри пример расчета площади основания пирамиды, заданной нашими условиями. Так как пирамида правильная, в ее основании лежит квадрат.
Площадь квадрата
рассчитывается по формуле: ,
где a – сторона квадрата. У нас она равна 6 см. Значит площадь основания пирамиды:![]()
Теперь остается только найти полную площадь многогранника. Формула площади пирамиды состоит из суммы площади ее основания и боковой поверхности.
Полная площадь боковой поверхности пирамиды состоит из суммы площадей его боковых граней.
В четырехугольной пирамиде различается два вида граней – четырехугольник в основании и треугольники с общей вершиной, которой образуют боковую поверхность.
Для начала потребуется рассчитать площадь боковых граней. Для этого можно использовать формулы площади треугольника, а можно также воспользоваться формулой площади поверхности четырехугольной пирамиды (только в случае, если многогранник правильный). Если пирамида правильная и в ней известна длина ребра a
основания и проведенной к нему апофемы h
, то:
![]()
Если по условиям даны длина ребра c
правильной пирамиды и длина стороны основания a
, то можно найти значение по следующей формуле:
Если же дана длина ребра в основании и противолежащий ей острый угол у вершины, то можно рассчитать площадь боковой поверхности по соотношению квадрата стороны a
к удвоенному косинусу половины угла α
:
Рассмотрим пример расчета площади поверхности четырехугольной пирамиды через боковое ребро и сторону основания.
Задача: пусть дана правильная четырехугольная пирамида. Длина ребра b
= 7 см, длина стороны основания a
= 4 см. Подставим заданные значения в формулу:
Мы показали расчеты площади одной боковой грани для правильной пирамиды. Соответственно. Чтобы найти площадь всей поверхности необходимо умножить результат на количество граней, то есть на 4. Если пирамида произвольная и ее грани не равны между собой, то рассчитать площадь необходимо для каждой отдельной стороны. Если в основании лежит прямоугольник или параллелограмм, то стоит вспомнить их свойства. Стороны у этих фигур попарно параллельны, а соответственно грани пирамиды будут также попарно одинаковы.
Формула площади основания четырехугольной пирамиды напрямую зависит от того, какой четырехугольник лежит в основании. Если пирамида правильная, то площадь основания рассчитывается по формуле , если в основании лежит ромб, то потребуется вспомнить, как находится . Ели же в основании лежит прямоугольник, то найти его площадь будет довольно просто. Достаточно знать длины сторон основания. Рассмотрим пример расчета площади основания четырехугольной пирамиды.
Задача: Пусть дана пирамида, в основании которой лежит прямоугольник со сторонами a
= 3 см, b
= 5 см. К каждой из сторон из вершины пирамиды опущена апофема. h-a
=4 см,h-b
=6 см. Вершина пирамиды лежит на одной линии с точкой пересечения диагоналей. Найдите полную площадь пирамиды.
Формула площади четырехугольной пирамиды состоит из суммы площадей всех граней и площади основания. Для начала найдем площадь основания:![]()
Теперь рассмотрим грани пирамиды. Они попарно одинаковы, потому что высота пирамиды пересекает точку пересечения диагоналей. То есть, в нашей пирамиде есть два треугольника с основанием a
и высотой h-a
, а также два треугольника с основанием b
и высотой h-b
. Теперь найдем площадь треугольника по известной формуле: ![]()
![]()
Теперь выполним пример расчета площади четырехугольной пирамиды. В нашей пирамиде с прямоугольником в основании, формула будет выглядеть так:
При подготовке к ЕГЭ по математике учащимся приходится систематизировать знания по алгебре и геометрии. Хочется объединить все известные сведения, например, о том, как вычислить площадь пирамиды. Причем начиная от основания и боковых граней до площади всей поверхности. Если с боковыми гранями ситуация ясна, так как они являются треугольниками, то основание всегда разное.
Как быть при нахождении площади основания пирамиды?
Оно может быть совершенно любой фигурой: от произвольного треугольника до n-угольника. И это основание, кроме различия в количестве углов, может являться правильной фигурой или неправильной. В интересующих школьников заданиях по ЕГЭ встречаются только задания с правильными фигурами в основании. Поэтому речь будет идти только о них.
Правильный треугольник
То есть равносторонний. Тот, у которого все стороны равны и обозначены буквой «а». В этом случае площадь основания пирамиды вычисляется по формуле:
S = (а 2 * √3) / 4.
Квадрат
Формула для вычисления его площади самая простая, здесь «а» - снова сторона:
Произвольный правильный n-угольник
У стороны многоугольника то же обозначение. Для количества углов используется латинская буква n.
S = (n * а 2) / (4 * tg (180º/n)).

Как поступить при вычислении площади боковой и полной поверхности?
Поскольку в основании лежит правильная фигура, то все грани пирамиды оказываются равными. Причем каждая из них является равнобедренным треугольником, поскольку боковые ребра равны. Тогда для того, чтобы вычислить боковую площадь пирамиды, потребуется формула, состоящая из суммы одинаковых одночленов. Число слагаемых определяется количеством сторон основания.
Площадь равнобедренного треугольника вычисляется по формуле, в которой половина произведения основания умножается на высоту. Эта высота в пирамиде называется апофемой. Ее обозначение - «А». Общая формула для площади боковой поверхности выглядит так:
S = ½ Р*А, где Р — периметр основания пирамиды.
Бывают ситуации, когда не известны стороны основания, но даны боковые ребра (в) и плоский угол при ее вершине (α). Тогда полагается использовать такую формулу, чтобы вычислить боковую площадь пирамиды:
S = n/2 * в 2 sin α.

Задача № 1
Условие. Найти общую площадь пирамиды, если в его основании лежит со стороной 4 см, а апофема имеет значение √3 см.
Решение. Его начинать нужно с расчета периметра основания. Поскольку это правильный треугольник, то Р = 3*4 = 12 см. Поскольку апофема известна, то можно сразу вычислить площадь всей боковой поверхности: ½*12*√3 = 6√3 см 2 .
Для треугольника в основании получится такое значение площади: (4 2 *√3) / 4 = 4√3 см 2 .
Для определения всей площади потребуется сложить два получившихся значения: 6√3 + 4√3 = 10√3 см 2 .
Ответ. 10√3 см 2 .
Задача № 2
Условие . Имеется правильная четырехугольная пирамида. Длина стороны основания равна 7 мм, боковое ребро — 16 мм. Необходимо узнать площадь ее поверхности.
Решение. Поскольку многогранник — четырехугольный и правильный, то в его основании лежит квадрат. Узнав площади основания и боковых граней, удастся сосчитать площадь пирамиды. Формула для квадрата дана выше. А у боковых граней известны все стороны треугольника. Поэтому можно использовать формулу Герона для вычисления их площадей.
Первые расчеты просты и приводят к такому числу: 49 мм 2 . Для второго значения потребуется вычислить полупериметр: (7 + 16*2):2 = 19,5 мм. Теперь можно вычислять площадь равнобедренного треугольника: √(19,5*(19,5-7)*(19,5-16) 2) = √2985,9375 = 54,644 мм 2 . Таких треугольников всего четыре, поэтому при подсчете итогового числа потребуется его умножить на 4.
Получается: 49 + 4*54,644 = 267,576 мм 2 .
Ответ . Искомое значение 267,576 мм 2 .
Задача № 3
Условие . У правильной четырехугольной пирамиды необходимо вычислить площадь. В ней известна сторона квадрата — 6 см и высота — 4 см.
Решение. Проще всего воспользоваться формулой с произведением периметра и апофемы. Первое значение найти просто. Второе немного сложнее.
Придется вспомнить теорему Пифагора и рассмотреть Он образован высотой пирамиды и апофемой, которая является гипотенузой. Второй катет равен половине стороны квадрата, поскольку высота многогранника падает в его середину.
Искомая апофема (гипотенуза прямоугольного треугольника) равна √(3 2 + 4 2) = 5 (см).
Теперь можно вычислять искомую величину: ½*(4*6)*5+6 2 = 96 (см 2).
Ответ. 96 см 2 .

Задача № 4
Условие. Дана правильная Стороны ее основания равны 22 мм, боковые ребра — 61 мм. Чему равна площадь боковой поверхности этого многогранника?
Решение. Рассуждения в ней такие же, как были описаны в задаче №2. Только там была дана пирамида с квадратом в основании, а теперь это шестиугольник.
Первым делом вычисляется площадь основания по указанной выше формуле: (6*22 2) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 см 2 .
Теперь необходимо узнать полупериметр равнобедренного треугольника, который является боковой гранью. (22+61*2):2 = 72 см. Осталось по формуле Герона сосчитать площадь каждого такого треугольника, а потом умножить ее на шесть и сложить с той, что получилась для основания.
Расчеты по формуле Герона: √(72*(72-22)*(72-61) 2)=√435600=660 см 2 . Вычисления, которые дадут площадь боковой поверхности: 660*6 = 3960 см 2 . Осталось их сложить, чтобы узнать всю поверхность: 5217,47≈5217 см 2 .
Ответ. Основания - 726√3 см 2 , боковой поверхности - 3960 см 2 , вся площадь - 5217 см 2 .